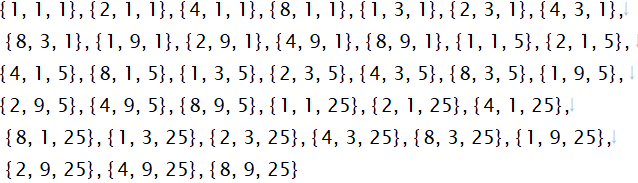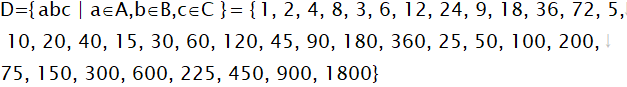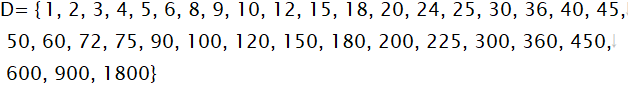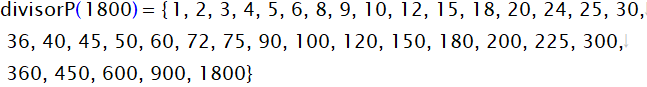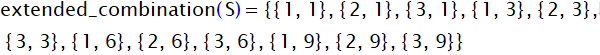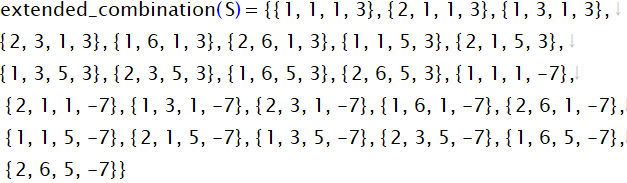約数を求めるアルゴリズムの改善
前回のメルマガでは、約数を求める簡素なアルゴリズムを説明しました。
マウスクリック
⇒
もう一度ご覧になりたい方は
常に最速のアルゴリズムを利用することが最良というわけでは
ありませんが、ここでは、カルキング機能の利用方法の説明のために
約数のさらなる高速化の方法を説明してみます。
ポイント
●素因数分解機能を利用する。
●カルキングでは素数表を内部で持っているため、素因数分解は高速で
実行できます。
「実行」メニューから素因数分解はできます。
1800の約数計算ではこの素因数分解のすべての情報が必要です。
これらの情報を参照するうえで、上記の計算結果は少し不便です。
カルキングでは、素因数分解のための関数があります。
代入定義により、R,Eの値が以下のように求まります。
基数部の値
指数部の値
このR,Eの値を使って、1800の36個すべての約数を作り出せます。約数の列挙に
これらの計算式を見ると指数計算が目立ちます、従って指数計算はあらかじめ
先に計算しておきましょう。
カルキングでは指数計算も集合演算ができます。
A,B,Cから1つづつ数値を使って、相異なる3組のすべてを列挙します。
注釈
これらの3組の整数値の積が1つの約数になります。約数には同じ数はありません。
以下の内包的集合定義式はこれを実行したものです。
sort関数で並べ替えましょう。
以上をスクリプトにまとめてみましょう。関数名をdivisorPとします。
検算
●divisorP関数の問題点
divisorP関数における問題点
★引数のnを素因数分解した時、素数の数が3に限定されている。
したがって内部変数を、p,q,rとかA,B,Cのように3個づつに限定して、アルゴリズム
を記述しています。素数の数が任意個に拡張拡張されると、スクリプトとして表現で
きなくなります。
●divisorP関数の改善
以下で作成す改善版の関数名はdivisorとします。
変数の個数を任意個に拡張する1つの方法は配列を使うことです。
これはプログラミングにおいては常套手段です。カルキングでは配列の代わりに行列
を使うことも可能です。
★プログラムの説明
divisorP関数の変数p,q,rの代わりに配列Pを導入した。
divisorP関数の変数A,B,Cの代わりに配列Sを導入した。
異なる素数の個数はmで表しています。
範囲変数 j =1..m を導入して、繰り返し代入文を実行させます。以下の2つが
繰り返し代入文になります。これによりプログラムが劇的に簡素化されています。
j の値を1つづつ増やしながらm回代入定義を実行します。
j の値を1つづつ増やしながらm回代入定義を実行します。
改善版作成で最も困難な部分は以下の部分の可変化です。
★任意個の組み合わせA,B,C,..から拡張組み合わせを作る方法
つまり
...
基本的アイデア
ステップ1
A,Bに関する拡張組み合わせ。
これは以下で与えられる。
もしSの要素が2つの場合はこれで終了
ステップ2
Sの要素が3つ以上の場合
とする。
Sの要素が3つの時は以下の式で求まる。
Sの要素が4つの時は以下の式で求まる。
厳密なアルゴリズム
nest_array関数はライブラリ関数です。
計算例
1次元配列を2次元化します。
配列内のすべての要素の積
補助関数PROD
補助関数PROD関数の計算例
extended_combination関数の計算例
の時
の時
の時
拡張組合せの定義
集合A,B,C,..の拡張組合せは以下の集合となります。
以上