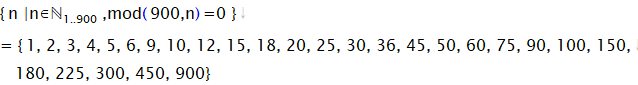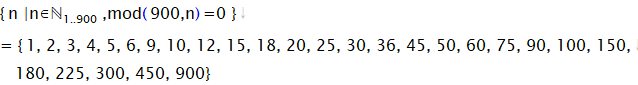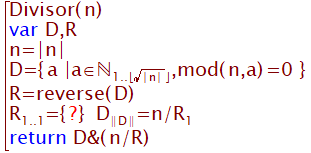因数分解を題材とした実験数学

まず初めに自然数の約数の求め方を説明します。その後、2次式の因数分解をたすき掛け
で解く方法をカルキングでシミュレートします。ここではカルキングの因数分解の解説
ではなく、あくまでもカルキングを利用して、実験を行うことが目的です。

●もっとも単純な方法

具体的に900の約数を求めます。内包的集合定義を利用すると簡単に計算できます。

この方法は１から900までのすべての整数値を総当たりで、調べる方法です。

わずか1行の簡単なもので、関数にする必要がないほど簡単です。

この式はmod関数を使い、余りが０になるすべての数値を列挙したものです。

今回の話題で取り上げる因数分解程度の約数では特に付け加えることはないのですが

不用意に1億の約数を求めようとすると、だめです。時間がかかりすぎます。

●改善策

ここまでの約数すべてをRとしたときに

説明

reverse関数は配列の並びを反転する

配列Rの先頭要素を削除

以下の約数もほぼ瞬時に求まります。

&演算子は2つの配列を連結する。

ここで対象とする2次式は次の条件を満たすこと

(1)2次の項の係数は必ず０以外の自然数であること

(2)すべての項の係数は共通因子を持たないこと

以下の式はこの条件を満たしています。

この解を以下の形式とします。

以下の手順では、リストの数を約半分にする工夫をしています。

D1の要素数が基数の時のために＋１が必要です。

たすき掛け方法の核心部分の式になります。

iとjがfor文における制御変数に相当するものです。

iは１～３、jは１～4 の範囲で条件部をチェックします。

D、Eはそれぞれ2次元配列になっているために2次元要素形式が使われています。

＿＿＿＿＿＿＿＿＿＿

課題の式の1次の項の係数が-60に条件

計算結果

従って

従って、因数分解の解が得られました。

以上をスクリプトの関数にまとめ上げます。

引数は2次式の係数です。

の時

答
え
の
見
栄
え
を
よ
く
す
る
た
め

●関数の実行結果

●他の例題

●正しくない例題１

理由

2次の項の係数が正の整数ではない

●正しくない例題２

理由

共通因子２が存在する。

このような時は共通因子を除いた式を因数分解すること

追記

簡略化してしまいました。

今回、約数関数Divisorを利用しましたが、カルキング365の次期イージーアップデート

では、これよりもさらに高性能化したdivisors関数を提供します。