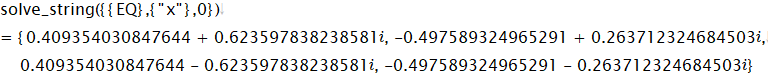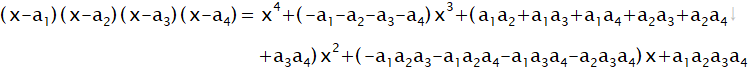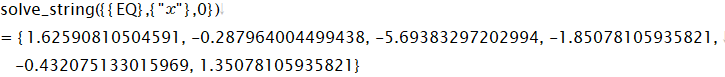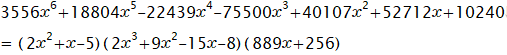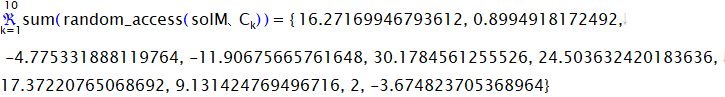ここでは高校数学程度を前提として、多項式の因数分解に関する一般アルゴリズムを
説明いたします。但しここでの方式は筆算向きではありません。ある程度の筆算で可能な

方式としてクロネッカーの方法がありますが、これに関しては後日、別の機会に説明する
ことにします。

ここで説明する方式は、多項式方程式の解を利用する方式です。このために筆算向きではないと

考えられます。つまりコンピュータ向きの方法です。ここで少し疑問が出てきます。

因数分解も難しいが、高次の多項式方程式を解くことも難しいのではと思われます。

しかし一般的にはニュートン法をはじめいくつかの方法が知られており、因数分解よりも

難易度が低いと考えられています。

因数分解の解を利用する方法としては、LLLアルゴリズムが有名ですが、今回はこれとは異なる方式です。

以下の多項式方程式の解をカルキングで求めてみましょう

カルキングの式番号を設定しておきます。

さらに(1)式には、複素数モードのプロパティーを

設定しておきます。

カルキングではこの方程式の解は3通りの方法で求めることができます。

●「実行」メニューの「方程式関連」の「一元多項式」で解を求める。

これがカルキングの一番利用される方法と思いますが、ここではこの方法は使いません。

●方程式コマンド　solveコマンドを利用する。引数は式番号の参照形式に限定されます。

「計算」メニューで解は変数ｘに設定されます。

●方程式関数　solve_string関数を利用する。引数は3つ必要です。。

因数分解関数では、方程式関数を利用します。

これらの変数を使って以下の4つの対称性のある式を計算してみます。

これら4つの小数はfract_judge関数で分数変換ができます。

以下が計算例です。

以上の現象は以下の計算式で了解されます。

以前メルマガで小数を分数近似するfract_apprx関数を紹介したことがあります。分数を見つけるとう点に
関しては同じですが、大きな違いがあります。

15桁の円周率の分数近似を求めてみると違いが明白になります。

このようにfract_judge関数は15桁の精度で、適切な分数は見つからないと判断しています。

方程式の解を利用する因数分解方式が有効であるための条件はfract_judg関数が作成できることです。

fract_judge関数を利用して、因数分解の一般解法を説明することは理にかなっています。しかしながら、

実はこの関数は使いません。因数分解への応用に関してはもっといい関数があるためです。

この関数は別途、いろいろな利用が可能です。次期カルキング３６５のイージーアップデートで

サポートする予定です。

分数判定法ではなく、整数判定法で、多項式方程式の解から、多項式の係数が導けます。

先ほどこの方程式の解が次の式から導けることを示しました。

ここからわかることは、これらの小数値に元の方程式の最高次の係数１７を

これらの小数から整数を導き出す、関数がint_judge関数です。この関数は、fract_judge関数

よりもはるかに簡単でかつ、はるかに高速です。

以下がこの関数を利用して計算した例です。

以下の具体的例でアイデアを説明しましょう。

●この方程式の解を求める。

先ほどの例と違って、すべて実根です。虚根があっても全く同じ方法でできます。

理解しやすいように、あらかじめ、今回の多項式の因数分解例を示しておきます。

この式から次の3つの方程式をとりだせます。

これら３つの方程式の解は、solve_string関数で求めた解と一致しています。

●方程式の解をもとに、1次の因子、2次の因子、3次の因子と順番に探します。

ステップ１

解の配列を変数solにセットします。

ステップ2

solの符号反転

代入定義

ステップ3

solの値を方程式の最高次数の3556倍する。このときの値をsolAに

代入しておく

代入定義

ステップ４

1次の因子を探す。

2番目だけが整数値です。

つまり1つの1次因子が見つかりました。

1次因子の具体的な式を求める。最高次の係数3556を分母として計算します。

この解になりえるのは以下の1次式のみです。

889x+256

この段階で次の2つの処理が必要です。

●最高次の係数の変更

●sol解から、2番目の解を削除する。

この代入定義で2番目が削除されます。

この段階でsolの要素数は5つになりました。

ステップ5

2次の因子を探す。

solの中から2つの組み合わせをすべて列挙する。

このリストをCとします。

先帆の計算によって最高次の係数は４になっています。

代入定義

Cの組み合わせでできる対の和が整数になるものを探します。

このような作業の時に便利なrandom_access関数があります。

期日もできます。

これら2組の数値の和はsum関数で記述できます。

Cのすべての組の、2組の和のリストを計算してみましょう。

このリストの中の9番目に２という整数が1つだけ存在しています。つまり2次式の因子は1つだけです。

最高次数の係数が４であったので、

これが見つかった2次式の1次の係数です。０次の係数は以下のように求まります。

従って０次の係数は

以上で見つかった2次式の数式は

今までの計算で、残る因子は3次式しかありえません。

3次式の多項式の2次、1次、0次の係数を求めてみましょう。

この段階での最高次の係数は２になっていました。

2次の係数

1次の係数

0次の係数

従って3次式の多項式は以下になります。

この式に最高次の係数２を掛ける

以上で因数分解のすべての因子が求まりました。

以上具体的例で多項式方程式の解を使った因数分解の方法を示しました。

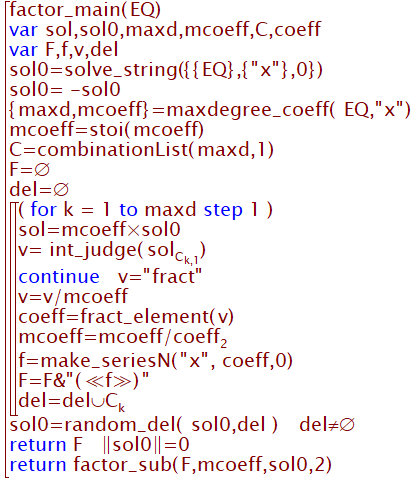
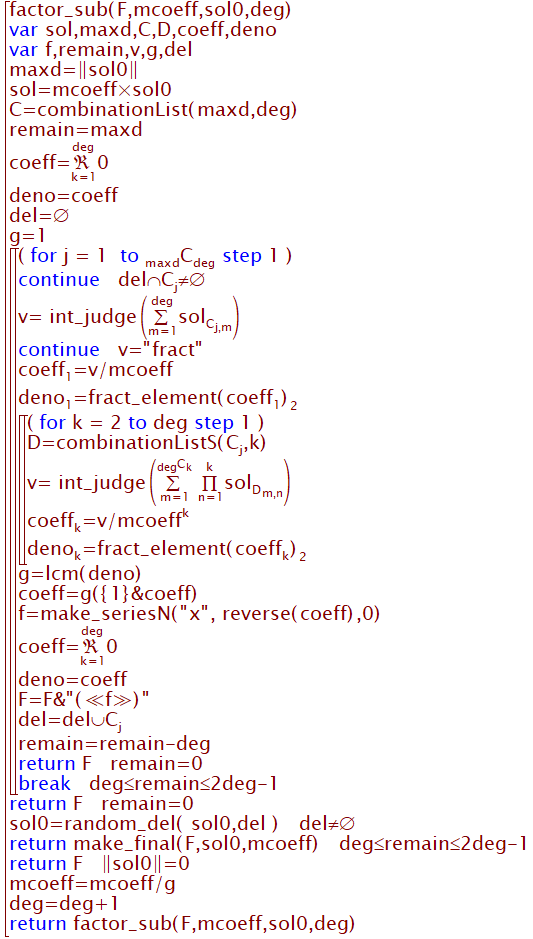
以下ではカルキングで作成した関数群を参考のために示します。

今回のプログラムは因数分解の方式の確認のため、仕様面では極めて荒削りのものになっています。

因数分解実行例1

関数への引数の形式  文字列型した方程式の形

因数分解関数の実行

因数分解実行例2

因数分解関数の実行

注

以上