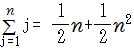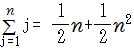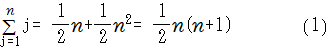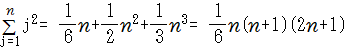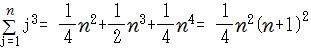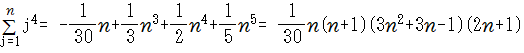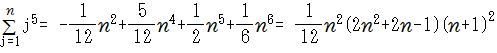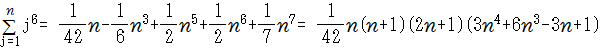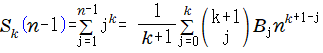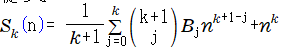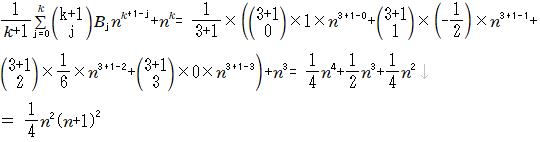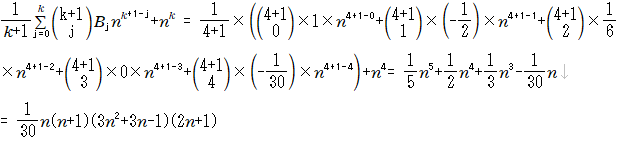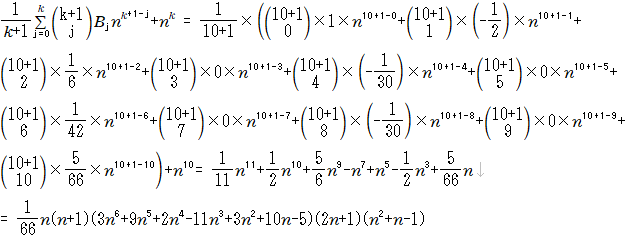べき乗和とベルヌーイ数

●カルキングでべき乗和公式を簡単に求める方法

分数モードの代数計算

注

ｎは未定義にしておくこと

もう少しなじみの式にするために続けて因数分解を実行した計算式は以下になります。

「再実行」

ちなみに総和部分をカルキングで展開することもできます。

「各種の展開」ー「総和　総乗」

余談

微積分の発見前に、放物線の面積や球の体積等をこれららの公式を使って計算していた

ためこれらの公式が特に重要だったと思われます。

関孝和も独立してこれらの公式を発見していたそうです。

●べき乗和の一般公式から個別のべき乗の公式を求める

すでに説明したように、カルキングでは簡単にべき乗和の公式が求まりますが、

ここでは、その解法の仕組みを説明することに主眼点があります。

2項係数とベルヌーイ数を使ってべき乗和の一般公式は以下のように書けます。

2項係数

ファウルハーバーの公式に関しては以下のサイトで説明されています。

https://ja.wikipedia.org/wiki/ファウルハーバーの公式

べき乗和の一般公式の応用として個別のべき乗の一般公式を求めてみましょう。

従って

以下の計算では下記の3つの操作を実行するだけです。

(1)べき乗数の設定

(2)置き換え計算

(3)代数計算

(4)代数計算

(2),(3),(4)の計算は1つの式の中で、連続して操作されます。

この関数Bの引数は添字型になっています。

この関数で使われているBernoulli_tableは、ライブラリファイルで既に定義されています。

例１

のケース

代入定義

例2

のケース

このケースは実演デモをご覧ください。

マウスクリック

↓

代入定義

●再実行機能を使って、10次のべき乗和の一般公式を求めてみましょう。

(1)上記の式をコピーします。

(2)ｋの値を10にして、代入定義を実行する。

(3)コピーした式を選択して、「再実行」すると、以下の式が得られます。

以上