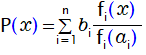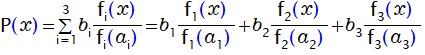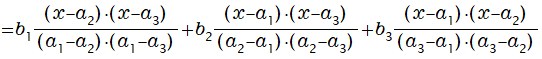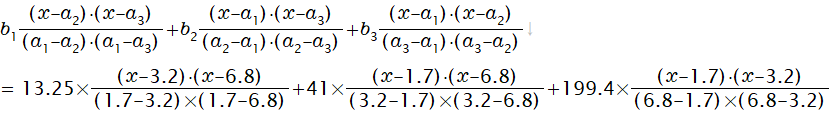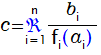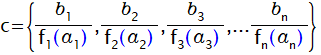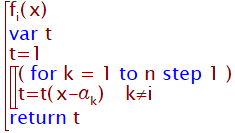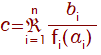n=3のケースを具体的に書き下してみましょう。

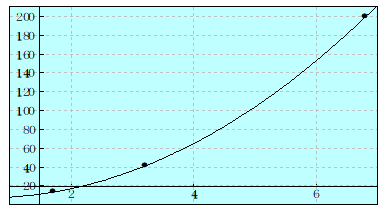
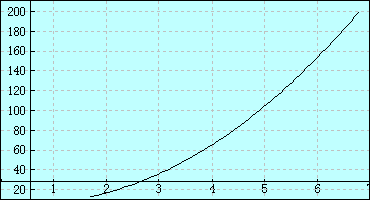
具体的数値で確認してみましょう。

確かに曲線上に3点が存在ます。

以上のようにラグランジュの補間公式を利用すれば

方程式を解いたりせずに近似多項式を求めることができます。

データ数が3個のように少ないときは、手計算でもできますが、データ数が増えると大変ですね。

実は、サンプル例題に掲載されています。

「データグラフ」－「ラグランジュ補間1-#.clk」

「データグラフ」－「ラグランジュ補間2-#.clk」

この2つの例題はラグランジュの補間公式の原型をもとに、補正された方式を採用しています。

以下では原形に従ったわかり易いスクリプトを示しておきます。

データ数を ｎ とします。

代入定義

代入定義

従って以下と等価になります。

代入定義

以上の準備で、ラグランジュの補間公式のためのスクリプトは以下のようになります。

下記スクリプトは多項式を直接に計算しているわけではありませんが、プログラミング上は等価なものになります。

以下のようにして関数グラフの「ノーマル型」で上で示した関数グラフと同様のものが得られます。

代入定義

代入定義

代入定義

代入定義

以上