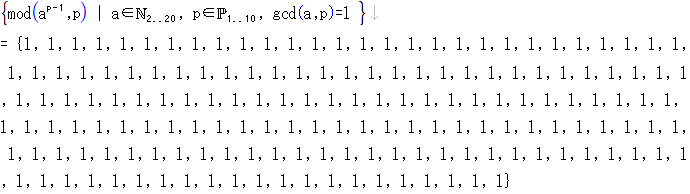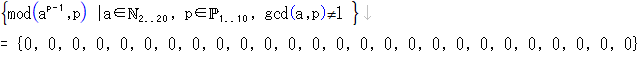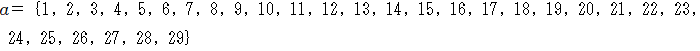フェルマーの小定理にまつわる実験数学

フェルマーの小定理の知名度はフェルマーの最終定理ほど知られてはいませんが、利用価値は逆
にはるかに高いです。

またある解説サイトによりますと、数学オリンピックでの出題傾向では最も高いそうです。

●フェルマーの小定理

注

このような≡とmodを使った式を合同式といいます。

あらゆる学問の初めは分類からスタートするように思いますが、合同式は整数の分
類に関する最も重要な式と考えられます。

●この式の意味

●サンプル例を使って、フェルマーの小定理の確認

カルキングのmod関数を利用して、確認します。

の時

の時

の時

の時

●フェルマーの小定理をより深く理解するための実験

実験１

代入定義

以下の内包的集合定義の式を計算すると、確かにすべて例外なく1になります。

実験２

aとｐが互いに素な数ではない時の計算

何と例外なく０になります。もちろんこれは証明できます。

実験３

この計算結果は、証明に結び付く驚くべき事実が分かります。

代入定義

代入定義

計算

関数定義

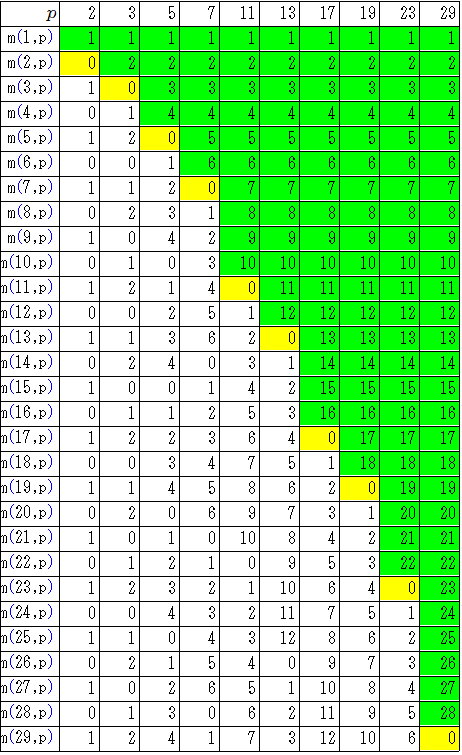
右の表のデータの色付きの

データは縦方向に見てください。
底のデータは０になっています。

データは縦方向に見ていくと

データの繰り返しパターンが

見られます。

は1,2,3,4のデータが繰り返さ

れています。

実は合同式の性質から次のこと

がわかります、

分かります。

6≡1

7≡2

8≡3

9≡4

が成り立ちます。この証明は最後の箇所をご覧ください。

以上でフェルマーの小定理が得られました。

補足

●帰納法による以下の式の証明

の時は自明です。

★1≦k≦p-1

この範囲ではｐはｋでは割り切れません。

したがって

は必ず整数になります。

帰納法の仮定により

従って

以上