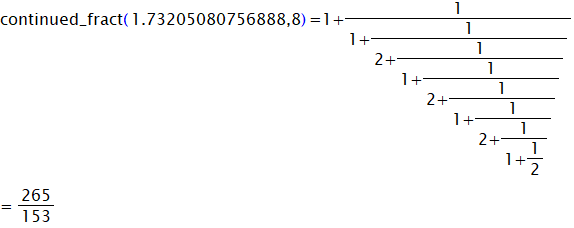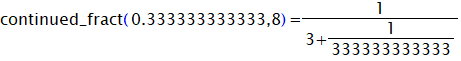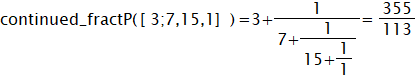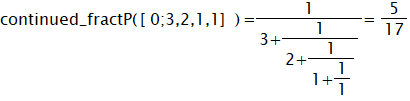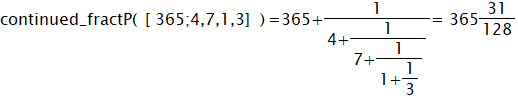連分数の応用 小数の分数近似
ここでは、単純な小数や循環小数だけではないもっと複雑な小数を適切な分数で近似するという
課題を考えてみましょう。循環小数に限れば簡単な方法がありますがここでは割愛します。
円周率の分数近似等が代表的な課題になります。
ここの課題は連分数の応用の代表的例になります。
カルキングではバージョン12から連分数機能がサポートされています。
しかし手間がかかりますが、分数機能があれば、連分数が計算できます。
以下のYouTubeサイトで小数を正則連分数に展開する動画が見れます。
⇒
こちら
以下に簡単にカルキングの正則連分数展開機能の実行例をします。
1.73205080756888の数値を8段の分数で展開した例です。
ちなみに
15桁での計算
このときの誤差を計算してみましょう。以下のように近似精度はかなり高いです。
continued_fract関数の出力はわかり易いが、表示面積を使いすぎます。
正則連分数では分子が常に1であるため以下の関数が簡潔でわかり易い。
この2つの計算例で分かりますが、先頭の要素は整数部分を表しています。
●次に以下のような循環小数風の例を計算してみましょう。
この意味をもっと分かりやすくするために8段の分数形式で計算してみましょう。
8段にならずに2段になります。
となります。
●15桁の円周率の例を計算してみましょう。
15桁の円周率の値
この連分数では292という比較的大きな数値が現れます。したがって、この数値以降を無視します。
正則連分数表現を繁分数に変換するcontinued_fractP関数を利用します。
従って以下の有名な円周率の近似値としての分数表現が求まりました。
● 0.294117647058825の例を計算してみましょう。
ここでは大きな値2352941176470が出現します。したがってこれ以降の値を無視します。
誤差を計算してみましょう。
● カレンダーにおける複雑な閏年の計算
複雑になっている原因は、太陽暦による1年の長さが次のようになっているからです。
この正則連分数には40の比較的大きな数値が現れます。従ってこれ以降を無視します。
カレンダー作成に関して、128年間の間に31年間は閏年にすれば調整ができるわけですが、
ほぼ均等に31回を決めるわかり易い方法は残念ながら見つかりません。しかし次の近似が見つかってい
ます。
誤差計算
この式はカレンダー的観点では次のように解釈できます。
4で割れる年は、1年を1日長くする(閏年)必要がある。
100で割れる年は4で割れるが、閏年をやめる。
400で割れる都市は、100でも割れるが、閏年にする。
この規約は比較的わかり易いですね。
...
●分数近似のカルキングスクリプトの作成
正則連分数の操作は配列とほぼ同じです。
配列データは中括弧で括られていますが、正則連分数は鍵括弧で括られています。
計算例
代数代入
要素参照
計算
計算
計算
要素削除
代数代入
計算
小数の分数近似の関数の作成例(カルキングver12及びカルキング365)
関数仕様
x: 小数点を含む数値
digit: 繁文数で近似したときの分数の段数
計算時のプロパティ
分数モード
計算例1
計算例2
以下のケースも一番簡素な円周率の分数近似の例です。
計算例3
以上