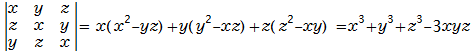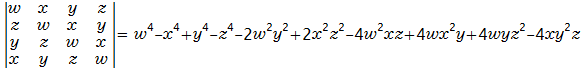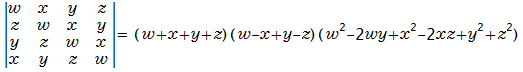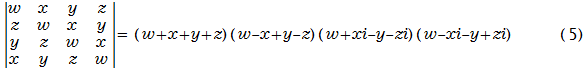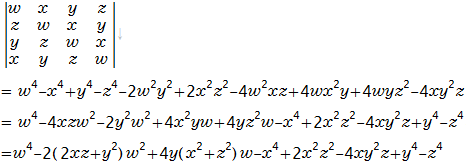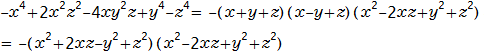4次方程式の解法
マウスクリック
3次方程式の解に関しては以下のサイトを参照してください。
↓
三次方程式の一般解
ここでの解法の基本的考え方は次の因数分解の公式をもとに導かれました。
これを複素数モードでさらに因数分解する。
他方の3次方程式の一般式は次のような2次の項のない3次方程式に変形できます。
従って次の2つの連立方程式の1つの解が求まれば（2）式から3つの解が求まりました。
この連立方程式は、見かけ状は2変数3次連立方程式ですが、実質は2次方程式の知識で
解けるものでした。
4次方程式もこのような仕組みで解きたいと思います。
そのためには、(1)式の因数分解の公式が必要です。
しかしながら以下の式は残念なことに因数分解はできません。
そこで4変数4次式の因数分解可能な式を探してみましょう。
この行列式は特徴的な形をしています。
行が変わるごとに循環しています。
この考えのもとにつぎの4次の行列式を計算してみましょう。
これらの行列式は巡回行列式（circulants）になっています。
驚くべきことにｎ次巡回行列式は複素数係数では常に因数分解できます！
整数の係数では以下のように因数分解できます。
複素数の係数では以下のように因数分解できます。(以下の因数分解の方法は下記のサイト)
マウスクリック
これらの詳しい導き方はこちらを参照してください。
↓
巡回行列式の因数分解
以上の準備の下に、4次方程式の一般解法を説明します。
4次方程式の標準形
4次方程式の一般形式は、常に以下の形に変形できます。
この連立方程式を解きやすくするために3番目の式を因数分解します。
改めて、連立方程式を作り直します。
新しい変数を導入する
(9)-(10)より
したがって
t,u,vに関して(6)、(7)、(8)の方程式を再構築します。
方程式(15),(16)から、変数ｔが消去できます。
式(17)のカッコを展開する。
(13)式を整頓すると以下の3次方程式が得られます。
このuの値は極め複雑になります。詳しくは以下のサイトをご覧ください。
マウスクリック
↓
三次方程式の一般解
3次方程式の一般解より、uが求まります。
(15)式より,以下のようにvが求められます。
(9)よりtがもとまります。
したがって、t,u,vが求まりました。
解
解き方は特に難しくないので、解だけ列挙します。
この解は2組求まりますが、1組だけで十分です。
(5)式の右辺より
従って4次方程式の最終解は以下の4組となります。
(15),(16),(17)のｘ、ｙ、ｚを利用します。
以上