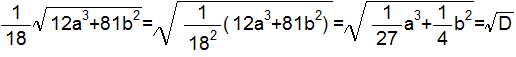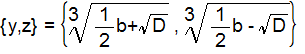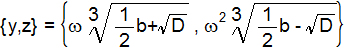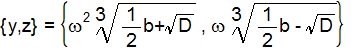特性方程式の解き方

y,zが未知数である以下の3次方程式の解法を説明します。

（１）式の両辺を3乗する。

以下のX,Yを導入する。

(2),(3）より、このY,Zに関する以下の連立方程式が作れます

（６）式からZを求め(7)に代入するとYに関する2次方程式になり、解けます。

（6）、（7）の連立方程式の解は次の２組となります。

ここでY,Zは二組の解が求まっていますが、初めの組の答えと2番目の組の答は、

対称になっています。

ルート記号を含む項は以下のように変形できます。

←

Dの定義より

従って

(8),(9)よりy,zが求まります。

注意すべきは、(4),(5)は、y、zに関する3次方程式となります。

このタイプの3次方程式の解　→

最も簡単な形をした3次方程式の解

よって、yに関しては以下の3つの解が導けます。

zに関しては以下の3つの解が導けます。

この解の組み合わせから方程式(1)を満たす解は以下の3組となります。

以上